Read about the Array Data Structures article before reading through this article.
Arrays are fundamental data structures in computer science and programming, offering a range of strengths, weaknesses, and Big-O complexities that impact their efficiency and usability.
Understanding the characteristics of arrays is crucial for choosing the right data structure for specific tasks and optimizing program performance.
This article delves into arrays' strengths, weaknesses, and Big-O complexities. We explore the benefits arrays provide, such as random and sequential access, simplicity of implementation, and cache-friendliness. Simultaneously, we address their limitations, including fixed size, insertion and deletion operations challenges, and inflexibility.
Additionally, we discuss the time complexities associated with common array operations, such as access, search, insertion, deletion, and resizing. By gaining insights into these aspects, programmers can make informed decisions when utilizing arrays and effectively balance trade-offs between efficiency and functionality in their applications.
Strengths
There are many advantages to using arrays, some of which are outlined below:
Fast lookups (random access)
Fast appends
Simple implementation
Cache friendliness
1. Fast lookups (Random access)
Retrieving the element at a given index takes O(1) time, regardless of the array's length.
For example:
int[] A = {-1, 7, 9, 100, 1072};
The array has five elements, and the length of the array is calculated using, A.lengthwhich is 5. As arrays are zero-indexed, the last element is accessed using A[A.length - 1] , which is A[4] as shown in the following sketch.

If we access array elements using the index, like A[0] or A[4], it takes a single unit of time or, in big-o terms, constant operation.
A[0]; // -1
A[3]; // 100
A[4]; // 1072
A[5]; // Index out of bounds exception, as there is no A[5] value.
All of the above operations consume a single unit of time: O(1) time.
2. Fast appends
Adding a new element at the end of the array takes O(1) time if the array has space.
Let us create an array with a capacity 5 and insert values 100 and 101 at indexes 0 and 1.
The following code explains it.
int[] A = new int[5];
A[0] = 100;
A[1] = 101;

Now if we were to insert a new value into the array, we could do A[2] = 200. Which inserts value 200 at the index 2. This operation consumes a single unit of time which is constant.

This is the reason the appends at the end are fast.
Enough talk. Here is a simple algorithm that creates an array with a size 5, and inserts 100, 101 values into the array. Finally, we insert an element at the array length.
import java.util.Arrays;
public class ArrayAppends {
public static void main(String[] args) {
int[] A = new int[5];
int currentLength = 0;
// Let us add 2 elements to the array
for (int i = 0; i < 2; i++) {
A[i] = i + 100;
currentLength++; // when i=1, length is set to 2
}
System.out.println(Arrays.toString(A)); // [100, 101, 0, 0, 0]
System.out.println("current array items length " + currentLength); // 2
System.out.println("Array capacity " + A.length); // 5
System.out.println(
"Element insert at end "
+ Arrays.toString(insertAtEnd(A, currentLength))); // [100, 101, 200, 0, 0]
}
// Inserting element at the end
public static int[] insertAtEnd(int[] A, int currentLength) {
A[currentLength] = 200;
return A;
}
}
/*
Outputs:
[100, 101, 0, 0, 0]
current array items length 2
Array capacity 5
Element insert at end [100, 101, 200, 0, 0]
*/
3. Simple Implementation
Arrays have a straightforward implementation in most programming languages, making them easy to understand and use.
4. Cache Friendliness
Elements in an array are stored contiguously in memory, which improves cache performance and can lead to faster access times.

Weaknesses
There are some disadvantages of using arrays, some of which are outlined below:
Fixed size.
Memory unused or wasted.
Size doubling.
Costly inserts
Costly deletes
1. Fixed-size
Arrays have a fixed size defined at the time of creation. Adding or removing elements beyond the initial size requires creating a new array and copying the existing elements, which can be inefficient.
You need to specify how many elements you will store in your array ahead of time. (Unless you're using a fancy dynamic array).
int[] A = new int[5]; // contains 5 elements
2. Memory unused or wasted
If an array's size is larger than the number of elements it contains, memory is wasted.
Imagine an array with a capacity of 5. We have two elements to store in this array, and then we are wasting three unfilled cells and a waste of memory, which means 3*(4 bytes) = 12 bytes of memory is wasted (integer takes 4 bytes).

3. Size doubling
Let us consider an array with a capacity of 5 elements. But the elements we want to store in this array are more, which means we have to double the size, create a new array, copy the old array elements and add new elements. The time complexity is O(n).

You will learn how to double the array size in the next lessons.
4. Costly inserts
Inserting/appending an element at the end of the array takes O(1) time. We have seen this in the strengths(fast appends).
But, inserting an element at the start/middle of the array takes O(n) time. Why? 🤔
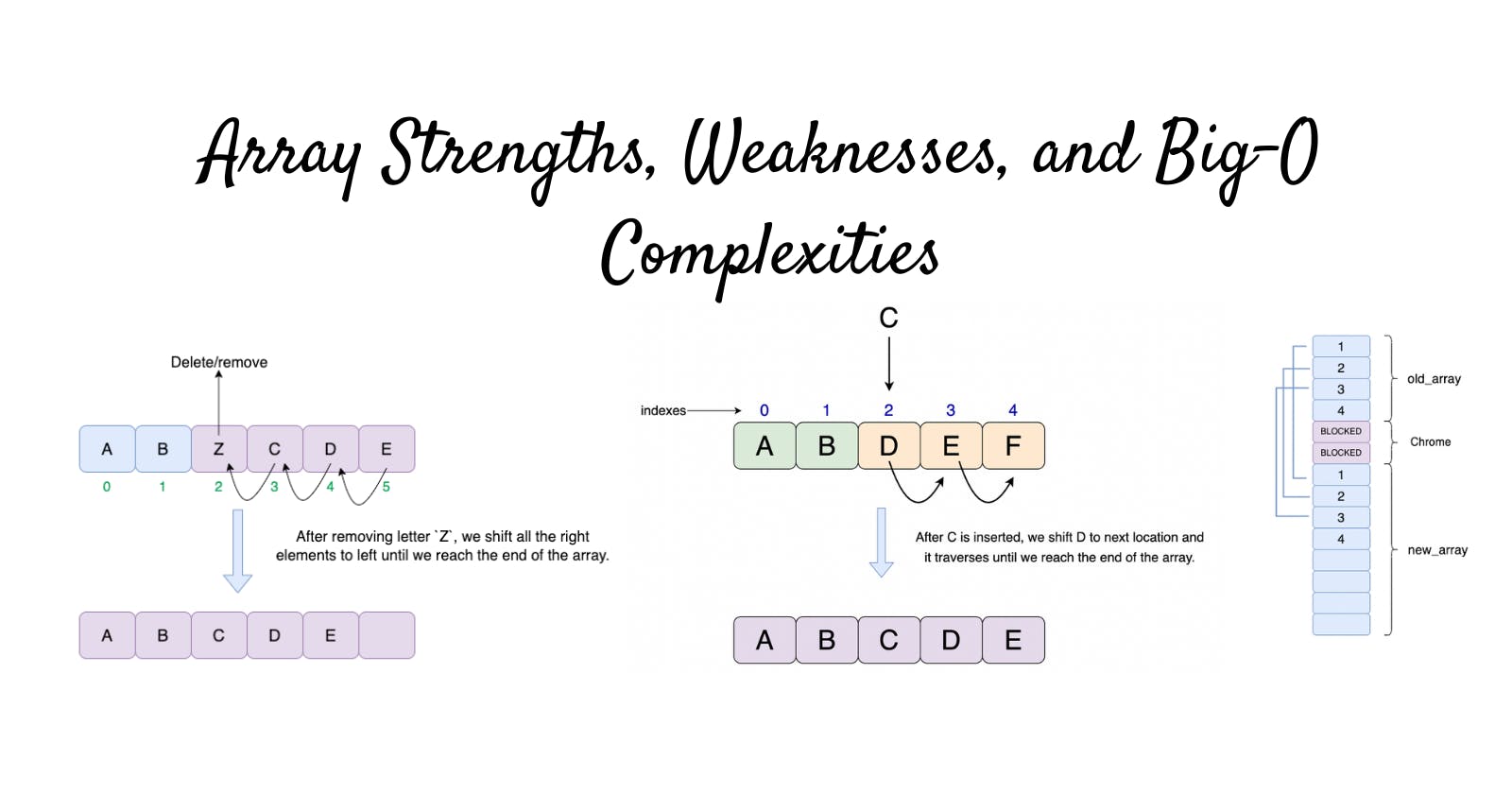
If we want to insert something into an array, first, we have to make space by "scooting over" everything starting at the index we're inserting into, as shown in the image. In the worst case, we're inserting into the 0th index in the array (prepending), so we have to "scoot over" everything. That's O(n) time.

Inserting an element at the 2nd index and moving the rest of the element right shift each once. The resultant array becomes – { A, B, C, D, E }.
In the next lessons, you will learn more about insertion and shifting algorithms, with clear explanations, code snippets, and sketches to understand why these inserts are expensive at the start and middle.
5. Costly deletes
Deleting an element at the end of the array takes O(1) time, which is the best case. In computer science, we only care about the worse case scenarios when working on algorithms. But, when we remove an element from the middle or start of the array, we have to fill the gap by scooting over all the elements after it. This will be O(n) if we consider a case of deleting an element from the 0th index.

Deleting an element at the 3rd index and filling the gap by left-shifting the rest of the elements; the resultant array becomes – { A, B, C, D, E }.
Big-O Complexities
| Operation | Complexity | Explanation |
| Lookup/Access a value at a given index | O(1) | Accessing an element by its index is a constant-time operation. |
| Search an element in an array | O(N) | Searching for a specific element in an unsorted array requires iterating through each element in the worst case. |
| Update a value at a given index | O(1) | Updating any element at any given index is always constant time. |
| Insert at the beginning/middle | O(N) | Inserting an element at the beginning or middle of the array requires shifting the existing elements, resulting in a linear time complexity. |
| Append at the end | O(1) | If the array has space available, inserting an element at the end takes constant time. |
| Delete at the beginning/middle | O(N) | Deleting an element from the beginning or middle of the array requires shifting the remaining elements, resulting in a linear time complexity. |
| Delete at the end | O(1) | Deleting the last element of an array can be done in constant time. |
| Resize array | O(N) | Resizing an array requires creating a new array and copying the existing elements, which takes linear time. |
The Big-O complexities mentioned above are for basic operations and assume an unsorted array. Some specialized data structures, such as Heaps or HashTables, can provide more efficient alternatives for specific use cases.
In the next lessons, you will learn more about array capacity vs. length, insertions, and deletion algorithms. They are the simplest yet most powerful and helps you when working on array problems.